NLP with Probalilistic Model
Probabilistic Model and how to use them to predict word sequences
This Technology is used to power auto-corrections and web search suggestions. The principle algorithms used are called
- Markov Models
- veterbi algorithm
Spelling Correction using Autocorrect
What is AutoCorrect?
AutoCorrect is a feature that changes misspelled words into the correct one. It uses the minimum edirt distance feaure to detect the candidates for correct word.
How does AutoCorrect work?
- 1. Identify a misspelled word
- 2. Find strings n edit distance away. These words could be random strings
- 3. Filter candidates. Keep only the real words from the previous steps.
- 4. Calculate word probabilities. Select the word that is most likely to occur in that context.
Identifying a misspelled word
Whether a word is mispelled or not is identified by it's presence in the dictionary. If the word is correct then it is found in the dictionary, if it is not then the autocorrect workflow gets executed for the misspelled word.
Finding strings that are n edit distance away from the input word
In this step we identify the words that are n-edit distance away from the input word. For example, dear is one edit distance away from deer. Edit operations are Insert, Delete and Switch (swap 2 adjacent letters) and Replace (replace one letter with another letter). By combining these operations on the original strings we can find all the strings that are n-edit distance away from the input string.
Filter Candidates
Not all of the words generated by these edits are actual words. Hence the filter mechanism nominates the actual word by matching the word with the vocabulary or dictionary. In this case we are only detecting the spelling errors and not the contexual errors.
Calculate word probabilities and find the most common words from the candidates
A body of text is called a Corpus, that hosts the vocabulary used in the particular piece of text. The count of the occurances of each word is calculated
for all the words in this corpus. Following is an example the word frequency for an example sentence
Sentence: A body of text is called a Corpus.
Word
Count
A
2
body
1
of
2
text
2
is
1
called
1
Corpus
1
The probability of a word is calculated by dividing the number of times the word appears divide by the total size of the corpus. $$ P(w) = \frac{C(w)}{V} \ \ \ \ P(text) = \frac{C(text)}{V} = \frac{2}{10} $$
Minimum Edit Distance
Minimum edit distance can be use to evaluate the diaance between two strings. Minimum edit distance is applied in various use cases such as Spelling Correction, Document Similarity, Machine Translation, DNA Sequencing and many more.
Minimum edit distance uses Dynamic programming and uses a matrix that takes account of how many edit operations are performed in order to change each character from the source word to target word. This minimum edit distance algorithm provides the mechanisms to get the candidates that are certain number of distance away from the input words. These candidates are then filtered for the most correct words.
Parts of Speech Tagging
POS Tagging using Viterbi Algorithm
Viterbi algorithm makes the use of Dynamic programming. Dynamic programmimg is an optimization technique that breaks down a big problem into smaller problems, comes up with an optimal solution of the mini problems and makes use of the optimal solution of the mini problem to solve the big problem.
Parts of speech refers to the lexical words in a sentence. Lexical terms are noun, verb, determiner and adverb in a sentence. We can make assumptions about the semantics of a sentence from Parts of Speech tags because POS tags describe the characteristic structure of the lexical terms. From Parts of Speech we can make assumptions about the semantics of a sentence because POS tags describe the characteristic structure of the lexical terms. Tags are used for coreference resolution. For example, in the sentences Eiffel Tower is located in Paris. It is 324 meters long. Eiffel Tower and Paris are both named entities and we can infer that it refers to Eiffel Tower. We can use the Markov Chain probabilistic Graphical Model to decode the parts of Speech in a sentence.
Parts of speech tagging can be used for:
- Identifying named entities
- Speech recognition
- Coreference Resolution
Markov Chain
Markov Chains are used to understand Parts of Speech tagging and Speech Recognition. Using In POS tagging use case using Markov Chain we try to undestand whether in a sentence given a word is a noun, how likely is it that the next word is a verb or a noun. If the given sentence is in English language then the probability of the next word being a verb is way greater than the the word being another noun.
A Markov Chain can be depicted as a Directive Graph. A Markov Chain can be depicted as a Directive Graph. A Graph consists of certain nodes or states and transitions or edge from one state to the other.
Markov Chains and POS Tags
While calculating the POS tagging, it is important to understand how likely one state will be transitioning to another state. The probability of going one state to the other is called Transition Probabilities. While calculating the POS tagging, it is important to understand how likely one state will be transitioning to another state. The probability of going one state to the other is called Transition Probabilities. A Markov Chain can be represented as a matrix of transition probabilities. Each row in the matrix represents transition probabilities of one states to all other states. All of the trasition probabilities of each row add up to 1. $$ \text{States} \ \ \ Q ={q_1, ....q_n} $$ $$ \text{Transition Matrix} \ \ A = \begin{bmatrix} a_{1,1} & \ \text{....} \ \ & a_{1,N} \\a{N + 1,1} & \ \text{....} \ \ & a_{N+1,N} \end{bmatrix} $$
Hidden Markov Model
Hidden Markov model is used decode the hidden state of a word. Hidden States is just the parts of speech of that word. For example the POS of the word "Call" is verb, and this constitute the hidden state of the word.
The Emission probabilities are another property of the Hidden Markov model. These describe the transition from the hidden states of your Hidden Markov model, to the observables or the words of the corpus. For example, the hidden state going(in this case which is a verb) could emmit to the observable like to and eat. Suppose the emission probability from the hidden states, verb to the observable, eat, is 0.5. This means when the model is currently at the hidden state for a verb, there is a 50 percent chance that the observable the model will emit is the word, eat.
Notation of Hidden Markov Model
States
Transition Matrix
Emmision Matrix
$ Q ={q_1, ....q_n} \ = \ \ $
$ A = \begin{bmatrix} a_{1,1} & \ \text{....} \ \ & a_{1,N} \\a_{N + 1,1} & \ \text{....} \ \ & a_{N+1,N} \end{bmatrix} \ = \ \ $
$ B = \begin{bmatrix}
b_{11} & \ \text{....} \ \ & b_{1V} \\ b_{N1} & \ \text{....} \ \ & b_{NV} \end{bmatrix} $
Calculating the Transition and Emmision Probabilities
1. Count occurances of tag pairs $C(t_{i-1}, t_i)$
2. Calculate probabilities using the counts
$ P(t_i|t_{i-1}) = \frac{C(t{i-1} - t_i)}{\sum_{j=1}^N \ C(t{i-1} - t_j} $
N-gram Models
A language model assigns the probability to a sequence of words. More like occuring sequences
will receive higher probabilities. More natural sequences in the real world gets higher probability.
N-Gram models are used to build language models. N-grams allows us to calculate the probabilities
of certain words occuring in a specific sequences.
P(I saw a van) > P(eyes awe of an)
N-gram Models and Probabilities
Bigram Probabilities
Corpus: I am happy because I am learning.
$ P(am|I) = \large{\frac{\text{I am}}{\text{C(I)}} = \frac{2}{2}} = 1 $
$ P(happy|I) = \large{\frac{\text{I happy}}{\text{C(I)}} = \frac{0}{2}} = 0 $
$ P(learning|am) = \large{\frac{\text{C(am learning)}}{\text{C(am)}} = \frac{1}{2}} $
Probability of a bigram: $ P(y|x) = \large{\frac{\text{C(x y)}}{\sum_{w} \ \text{C(x \ w)}} = \frac{C(x \ y)}{C(x)}} $
N-gram Probability:
$ P(W_N|W^{N-1}_{1}) = \large{\frac{C(W^{N-1}_{1} W_{N})}{C(W^{N-1}_{1})}} $
$ C(W^{N-1}_{1} W_{N}) = C(W^{N}_{1}) $
Probability of a Sequence
Using n-gram probabilities, a model for an entire sentence can be built. The probability of an entire
sentence can be built using the Conditional probability and Chain rule. Following is theconditional
probability of the word B
$$ P(B|A) = \frac{P(A, B)}{P(A)} \ \rightarrow P(A, B) = P(A)P(B|A) $$
The probability and chain rule can be used in order to calculate the probability of a sentence
$$ P(B|A) = \frac{P(A,B)}{P(A)} $$
$$ P(A,B,C,D) = P(A)P(B|A)P(C|A, B)P(D| A, B, C) $$
The probability of each word is calculated by product of the probability of all the predecessor
words occured before the word in the sequence
Given a sentence, how to calculate its probabilities?
P(The teacher drinks tea) = ?
P(The teacher drinks tea) = P(The)P(teacher|The)P(drinks|The teacher)P(tea|The teacher drinks)
Since the natural language is highly variable, the exact sequence of the query sentence may not
be found in the training corpus, hence the probability of that input sequence will be zero.
As the sentence gets longer and longer, the likelihood of its words will occur in a definite
sequence becomes smaller and smaller.To resolve this issue we can shrink the width of the
scanning window, instead of looking at all the words before a specific word we can look at the
previous word or the previous two words.
P(tea | the teacher drinks) $ \approx $ P(tea | drinks)
The bi-gram probabilities are calculated instead of calculating the whole sentence together.Bi-gram probabilities
are the product of the conditional probabilities of bi-grams occuring in a sentence.
P(The)P(teacher|The)P(drinks|teacher)P(tea|The drinks)
The Markov Assumption
We can apply the Markov Assumption in this context. The Markov assumption states the probability of a word depends only on its limited history of length n. Instead of using a bi-gram model, a tri-gram or an n-gram model can also be applied.
Approximation of sequence probability
Markov Assumption:
only last N words matter
Bigram
$ P(w_n | w^{n-1}{1}) \approx P(w_n | w_{n-1}) $
N-gram
$ P(w_n | w^{n-1}{1}) \approx P(w_n | w^{n-1}{n-N+1}) $
Word Embeddings
Word Embeddings are also known as the word vectors. A word embedding can be represented as a Matrix, in which each vector represents a word. One of the other word representations is One-hot vectors, but One-hot vector representation can be sparsed and does not offer any embedded meaning of the word it represents.
Word vector and Word meaning
With word embedding we can encode meaning of a vector even in a low dimensional space. Following is a one-dimensional space and the positive words are plotted at the right side of 0 and the negative words are plotted at the left side of 0
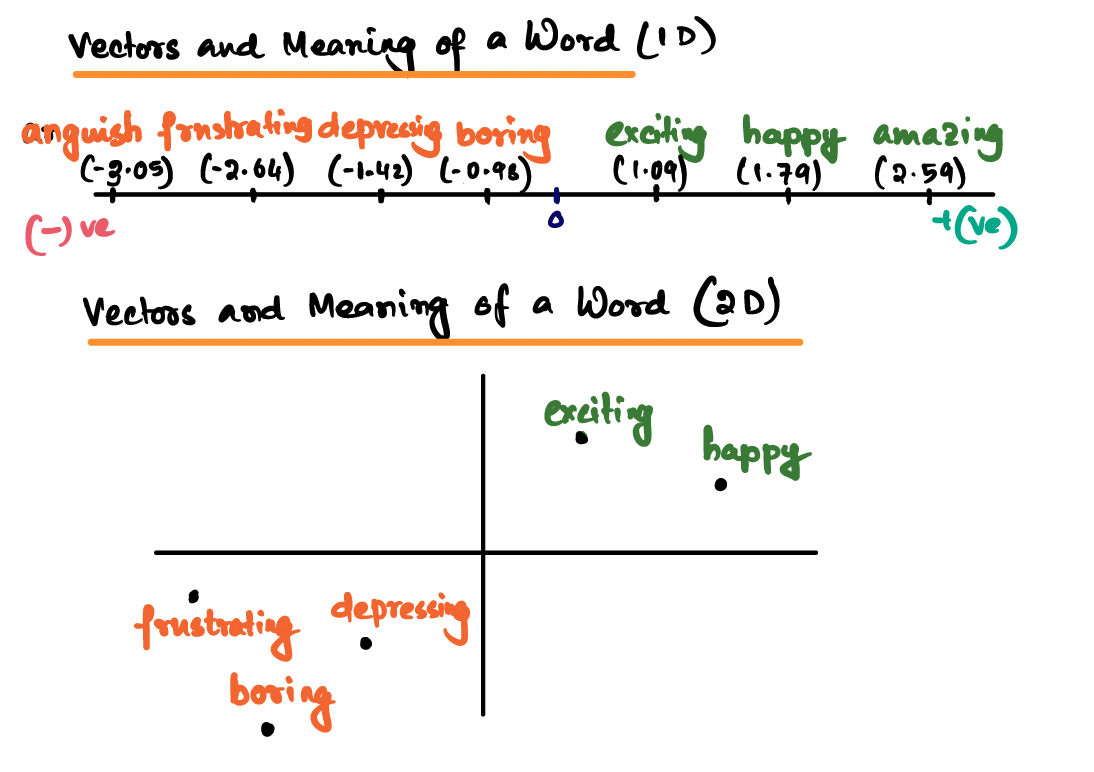 |
Word vector and Word meaning
The Corpus that is used to create an embedding will affect the nature of Embedding. Word Embedding process requires a Corpus and an Embedding method. The corpus contains the words organized in the same way as they would be used in the context of interest. A context gives meaning to each word embedding. The corpus would be a general purpose sets of documents such as, Wikipedia articles, or it could be more specialist such as, an industry, or enterprise specific corpus to capture the nuances of the context. For NLP use cases on legal topics, contracts, and law books as the corpus can be used, the embedding method creates the word embeddings from the corpus.
An embedding method creates the word embedding from the corpus. There are several ways to create a word embedding. Word2Vec is a model that uses a shallow neural network to create a word embedding. The objective of the model is to learn to predict a missing word given a surrounding word. Other significant models are GloVe which uses factorizing the logarithm of the corpuses word co-occurrence matrix and FastText that takes into account the structure of wordsby representing words as an n-gram of characters.
Word embeddings are used widely by large language models to understand long sequence of words and can be considered as foundational building blocks of Natural Language Processing.